Bu başlık altında daha önceki başlıklarda incelediğimiz Veri Bilimi Metodolojileri’nin sonraki iki aşaması olan Modelleme ve Değerlendirme aşamalarına göz atacağız.
Modelleme
Modelleme, veri bilimi metodolojisindeki, veri bilimcisinin sosu örnekleme ve daha fazla baharata ihtiyacı olup olmadığını belirleme şansına sahip olduğu aşamadır!
Bu aşama iki temel soruyu yanıtlamaya yöneliktir:
1- Veri modellemenin amacı nedir?
2- Bu sürecin özellikleri nelerdir?
Veri Modelleme, hem tanımlayıcı hem de tahmine dayalı modeller geliştirmeye odaklanır.
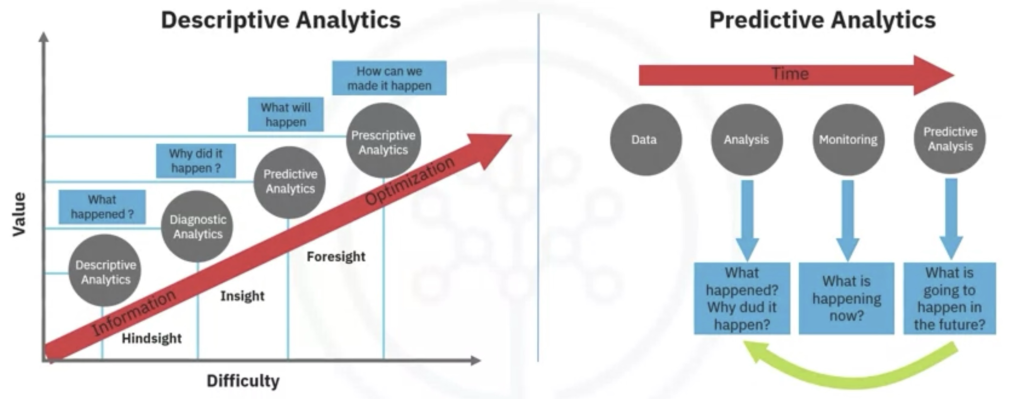
Tanımlayıcı bir model, şu tür örnekleri inceleyebilir: Eğer bir kişi bunu yaptıysa, muhtemelen bunu tercih edecektir. Tahmine dayalı bir model ise, evet/hayır gibi ikili(binary) sonuçlar vermeye çalışır. Bu modeller, istatistiksel olarak yönlendirilen veya makine öğrenimi tarafından yönlendirilen analitik yaklaşıma dayanmaktadır.
Veri bilimcisi, tahmine dayalı modelleme için bir eğitim seti kullanacaktır. Bir eğitim seti, sonuçların zaten bilindiği bir dizi tarihsel veridir. Eğitim seti, modelin kalibre edilmesi gerekip gerekmediğini belirlemek için bir gösterge görevi görür.
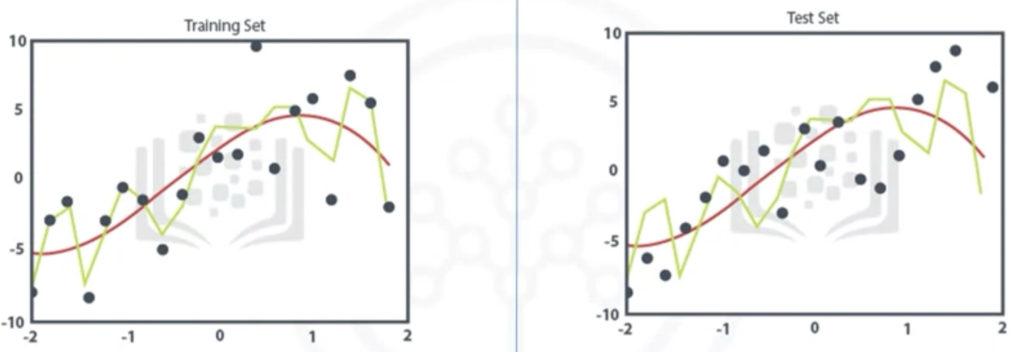
Bu aşamada, veri bilimcisi, kullanılan değişkenlerin gerçekten gerekli olduğundan emin olmak için farklı algoritmalarla çalışacaktır.
Veri Derleme, Veri Hazırlama ve son olarak Modellemenin başarısı, eldeki problemin anlaşılmasına ve uygun analitik yaklaşımın benimsenmesine bağlıdır. Veriler, sorunun yanıtını destekler ve yemek pişirmedeki malzemelerin kalitesi gibi sonuca zemin hazırlar. Sonucun sağlam olmasını sağlamak için her adımda sürekli iyileştirme ve ince ayar gereklidir.
John Rollins’in Tanımlayıcı Veri Bilimi Metodolojisi’nde yaklaşım 3 şeyi yapmaya yöneliktir: İlk olarak, eldeki soruyu anlayın. İkinci olarak, sorunu çözmek için bir analitik yaklaşım veya yöntem seçin ve üçüncüsü, verileri elde edin, anlayın, hazırlayın ve modelleyin. Nihai hedef, veri bilimcisini soruyu cevaplamak için bir veri modelinin oluşturulabileceği bir noktaya taşımaktır.
Uygulama:
Daha önce örneklediğimiz Konjestif Kalp Yetmezliği olayını veri bilimi metodolojisinde modelleme aşamasına uygulayalım. Bu vakada, model oluşturmanın birçok yönünden biri olan modeli geliştirmek için parametre ayarlama konusunu inceleyeceğiz.
Hazırlanan bir eğitim seti ile Konjestif Kalp Yetmezliği vakalarının hastahaneye yeniden başvurusu için ilk karar ağacı sınıflandırma modeli oluşturulabilir. Yeniden başvuru ihtimali yüksek riskli hastaları arıyoruz. Bu nedenle Konjestif Kalp Yetmezliği’nin yeniden kabulü “Evet” olacak.
| Model | Göreli Maliyet E:H | Genel Doğruluk (E & H için doğruluk yüzdesi) | Duyarlılık (E doğruluğu) | Özgüllük (H doğruluğu) |
| 1 | 1:1 | %85 | %45 | %97 |
| 2 | 9:1 | %49 | %97 | %35 |
| 3 | 4:1 | %81 | %68 | %85 |
1 numaralı modelde, evet ve hayır sonuçlarını sınıflandırmada genel doğruluk %85’dir. Bu başarı oranı kulağa hoş geliyor, ancak Duyarlılık(E doğruluğu) sütununda “evet” sonucunun sadece %45’ini temsil ettiği görülüyor. Gerçek geri kabuller doğru bir şekilde sınıflandırılmıştır, bu da modelin çok doğru olduğu anlamına gelir. Ancak bir sorunumuz olduğu açık ve bu akla şu soruyu getiriyor: “Evet sonucunu tahmin etmede modelin doğruluğu nasıl geliştirilebilir?”
Karar ağacı sınıflandırması için kullanılabilecek en iyi parametre, yanlış sınıflandırılan evet ve hayır ilişkili sonuçlarıdır. Bunu şöyle düşünün: hastanın başvurusu doğru olduğunda, ancak yeniden başvuru olarak kabul edilmediğinde, yani yeniden kabul edilmeme durumu yanlış sınıflandırıldığında, o hastanın riskini azaltmak için harekete geçilmesi gerekecek, ve bu hatanın maliyeti boşa yapılan müdahale olacaktır. İstatistikçiler buna “Tip-I Hata” veya “Yanlış Pozitif” diyor. Ancak gerçek bir yeniden kabul yanlış sınıflandırıldığında ve bu riski azaltmak için herhangi bir önlem alınmadığında, o zaman bu hatanın maliyeti hastanın yeniden kabulünün gerekmesi ve artı hastanın travmasıdır. Bu “Tip-II Hata” veya “Yanlış Negatif”tir. Dolayısıyla, iki farklı yanlış sınıflandırma hatasının maliyetleri farklı olacaktır.
Bu nedenle, evet ve hayır sonuçlarını yanlış sınıflandırmanın göreli ağırlıklarını ayarlamak mantıklıdır. Varsayılan 1’e 1’dir, ancak karar ağacı algoritması, “evet” için daha yüksek bir değerin ayarlanmasına izin verir.
İkinci model için göreli maliyet 9’a 1 olarak belirlendi. Bu çok yüksek bir orandır, ancak modelin davranışı hakkında daha fazla fikir verir. Bu sefer model, “evet”‘in %97’sini doğru bir şekilde sınıflandırdı, ancak “hayır” için çok düşük bir doğruluk söz konusu, yalnızca %49’luk bir genel doğrulukla sınıflandırılmış. Bu açıkça görülüyor ki iyi bir model değil. Bu sonuçla ilgili sorun, tekrar başvuru olarak kabul edilmeyecek olan hastalar için gereksiz ve maliyetli müdahaleyi önerecek çok sayıda yanlış pozitife neden olacaktır. Bu nedenle, veri bilimcisinin evet ve hayır doğrulukları arasında daha iyi bir denge bulmak için yeni bir model denemesi gerekir.
Üçüncü model için, göreli maliyet daha makul bir oranla 4’e 1 olarak ayarlandı. Bu sefer, istatistikçiler tarafından duyarlılık olarak adlandırılan yalnızca “evet” üzerinde %68 doğruluk ve özgüllük olarak adlandırılan “hayır” için %85 doğruluk oranı, genel olarak %81 doğrulukla elde edildi. Bu, yanlış sınıflandırılan evet ve hayır sonuç parametresinin göreli maliyetini ayarlayarak oldukça küçük bir eğitim seti ile elde edilebilecek en iyi dengedir.
Elbette daha iyi sonuçlar için modelleme üzerinde; diğer değişkenlerin bazılarını yeniden tanımlamak, temel bilgileri daha iyi temsil etmek ve böylece modeli geliştirmek için veri hazırlama aşamasına geri yineleme de dahil olmak üzere çok daha fazla çalışma yapılabilir.
Değerlendirme
Bir modelin değerlendirilmesi, model oluşturma ile eşzamanlı yürütülür. Modelleme ve değerlendirme aşamaları yinelemeli olarak yapılır. Model değerlendirmesi, model geliştirme sırasında ve model dağıtılma(deploy) aşamasından önce gerçekleştirilir.
Değerlendirme, modelin kalitesinin değerlendirilmesini sağlar, ancak aynı zamanda ilk talebi karşılayıp karşılamadığını görmek için bir fırsattır. Değerlendirme şu soruya cevap verir: Kullanılan model gerçekten ilk soruya cevap veriyor mu yoksa düzenlenmesi gerekiyor mu?
Model değerlendirmesinin iki ana aşaması olabilir;
İlki, modelin amaçlandığı gibi çalıştığından emin olmak için kullanılan Tanısal Ölçümler (Diagnostic Measures) aşamasıdır. Tanısal Ölçümler(Diagnostic Measures) modelin performansını değerlendirmek için kullanılan metriklerdir. Bu ölçümler, modelin ne kadar iyi öğrendiğini, veriye ne kadar iyi uyduğunu ve gelecekteki veriler üzerinde ne kadar iyi genelleme yapabileceğini anlamamıza yardımcı olur.
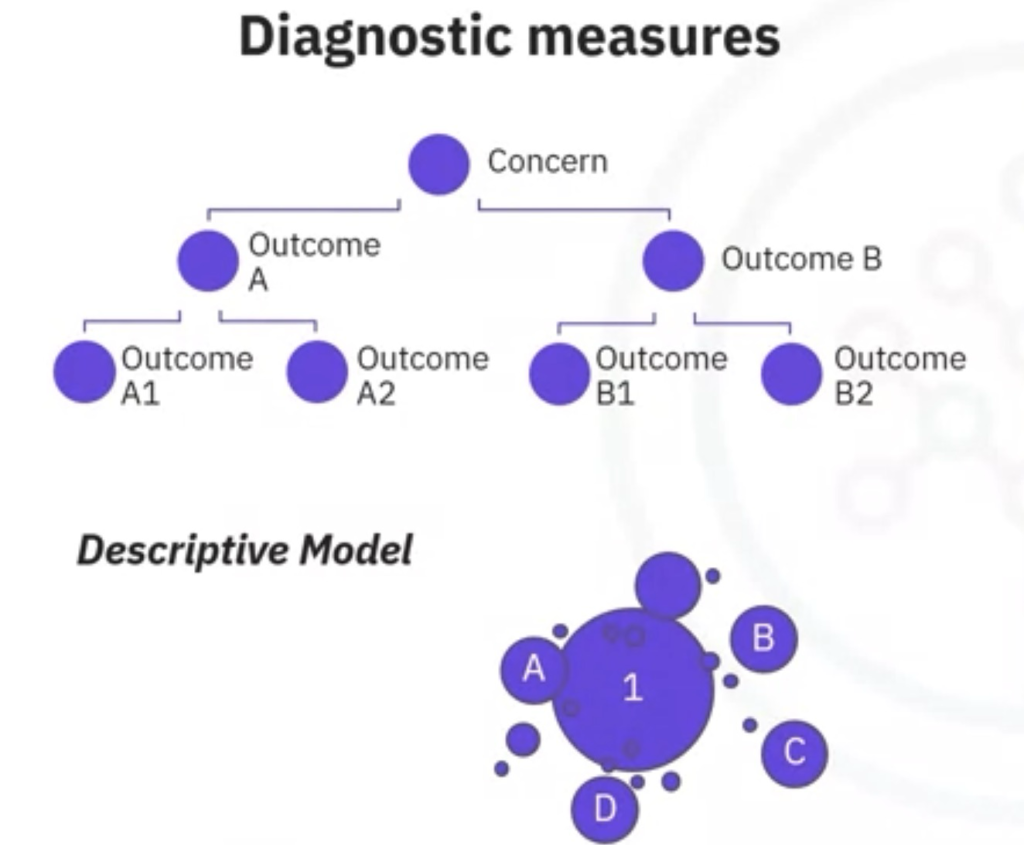
Model tahmine dayalı bir modelse, modelin verebileceği cevabın ilk tasarımla uyumlu olup olmadığını değerlendirmek için bir karar ağacı kullanılabilir. Bu yaklaşım düzenleme gerektiren alanların nerede olduğunu görmek için kullanılabilir. Model, ilişkilerin değerlendirildiği tanımlayıcı bir modelse, sonuçları bilinen bir test seti uygulanabilir ve model gerektiği gibi geliştirilebilir.
Neden Önemlidirler?
- Modelin Güvenilirliği: Tanısal ölçümler sayesinde modelin çıktılarının ne kadar güvenilir olduğu anlaşılır.
- Modelin İyileştirilmesi: Hangi alanlarda iyileştirme yapılması gerektiği konusunda yol gösterirler.
- Model Seçimi: Farklı modellerin performansını karşılaştırmak için kullanılırlar.
- Overfitting/Underfitting Tespiti: Modelin veriye aşırı uyum sağlaması (overfitting) veya yeterince uyum sağlayamaması (underfitting) durumlarını tespit ederler.
Örnek Tanısal Ölçümler:
- Confusion Matrix: Sınıflandırma problemlerinde modelin tahminlerini gerçek değerlerle karşılaştıran bir tablo. Doğru pozitif, yanlış pozitif, doğru negatif ve yanlış negatif gibi değerleri içerir.
- ROC Eğrisi: Sınıflandırma modellerinin performansını görselleştirmek için kullanılan bir grafik. Eğrinin altında kalan alan (AUC) değeri, modelin ne kadar iyi ayırt edebildiğini gösterir.
- Hassasiyet(Precision), Duyarlılık(Recall), F1-Score: Sınıflandırma problemlerinde kullanılan diğer önemli metriklerdir. Precision, modelin pozitif olarak tahmin ettiği örneklerin ne kadarının gerçekten pozitif olduğunu, recall ise tüm pozitif örneklerin ne kadarının model tarafından doğru olarak tahmin edildiğini gösterir. F1-score ise precision ve recall değerlerinin harmonik ortalamasıdır.
- Mean Squared Error (MSE): Regresyon problemlerinde modelin gerçek değerlerden ne kadar uzaklaştığını ölçen bir metriktir.
- R-squared: Regresyon modelinin açıkladığı varyansın toplam varyansa oranını gösterir.
- Mean Absolute Error (MAE): Regresyon problemlerinde mutlak hata değerlerinin ortalamasıdır.
Bir bankanın kredi tahmin modeli düşünelim. Bu model, bir müşterinin kredi başvurusunu değerlendirerek, müşterinin krediyi geri ödeyip ödemeyeceğini tahmin eder. Modelin performansını değerlendirmek için confusion matrix, ROC eğrisi ve F1-score gibi metrikler kullanılabilir. Bu metrikler sayesinde bankanın yanlış pozitif (kredi vermeye uygun olmayan müşteriye kredi verilmesi) veya yanlış negatif (kredi vermeye uygun olan müşteriye kredi verilmemesi) gibi hatalar yapma olasılığı hakkında bilgi sahibi olunur.
Kullanılabilecek ikinci değerlendirme aşaması, istatistiksel anlamlılık testidir.
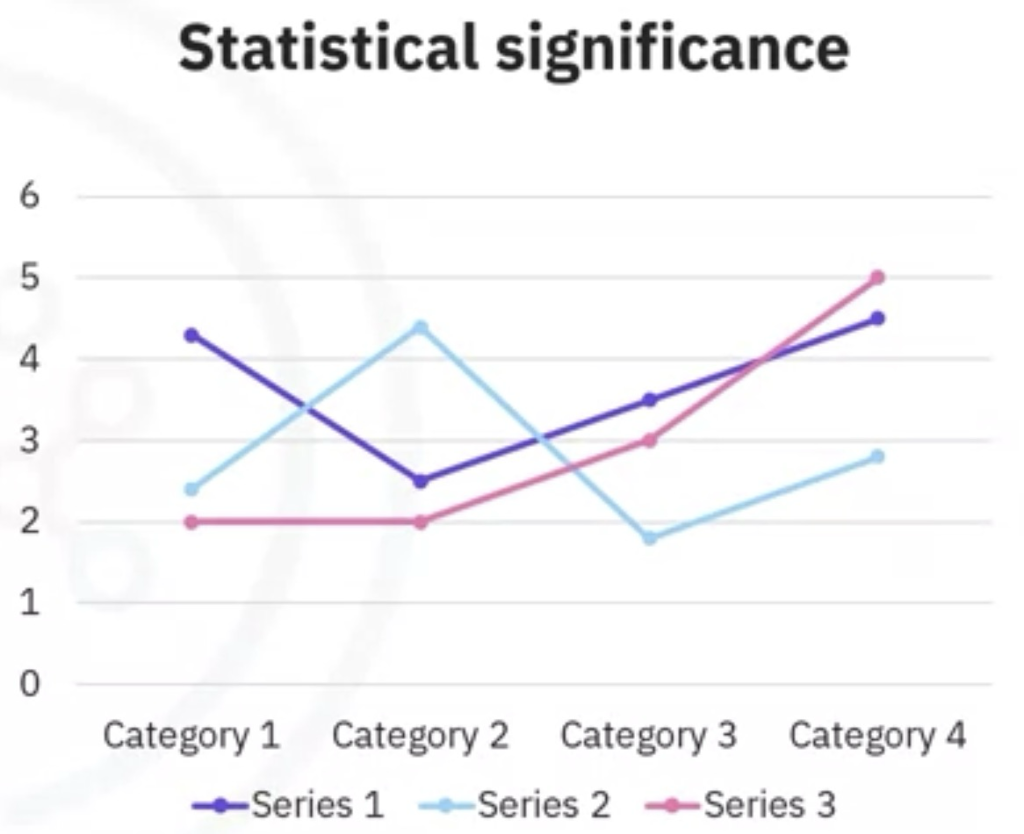
Bu tür bir değerlendirme, verilerin model içinde uygun şekilde işlendiğinden ve yorumlandığından emin olmak için modele uygulanır. Bu aşama, cevap ortaya çıktığında gereksiz ikinci tahminlerden kaçınmak için tasarlanmıştır.
Şimdi, veri bilimi metodolojisinde “Değerlendirme” bileşenini uygulayabilmemiz için örnek olay incelememize geri dönelim.
Uygulama:
Model oluşturmadaki parametrelerden birinin ayarlanmasına dayalı bir tanı ölçüsü aracılığıyla en uygun modeli bulma işlemine göz atalım. Burada spesifik olarak, “evet” ve “hayır” sonuçlarını yanlış sınıflandırmanın göreli maliyetini nasıl bulacağımızı göreceğiz.
| Model | Göreli Maliyet E:H | Doğru Pozitif Oranı (Hassasiyet) | Özgüllük (H doğruluğu) | Yanlış Pozitif Oranı (1-Özgüllük) |
| 1 | 1:1 | %45 | %97 | %3 |
| 2 | 1.5:1 | %60 | %92 | %8 |
| 3 | 4:1 | %68 | %85 | %15 |
| 4 | 9:1 | %97 | %35 | %65 |
Bu tabloda gösterildiği gibi, dört farklı göreceli yanlış sınıflandırma maliyeti ile dört model oluşturulmuştur. Gördüğümüz gibi, bu model oluşturma parametresinin her değeri, hayır tahmininde daha düşük doğruluk pahasına yani artan bir yanlış-pozitif oranına karşın evet tahminindeki doğruluğun gerçek-pozitif oranını veya hassasiyetini arttırır. Yani, göreli maliyet sütununda H karşısında E oranı arttıkça Doğru Pozitif Oranı sütununda artış gözlemlendiğinden bahsediyoruz. Ancak aynı zamanda Yanlış Pozitif Oranında da bir artış görülüyor.
O zaman sorumuz şudur; “Bu parametreyi düzenlemeye dayanan en iyi model hangisidir?”
Bütçeyle ilgili nedenlerle, risk azaltıcı müdahale Konjestif Kalp Yetmezliği hastalarının çoğuna veya tamamına uygulanamamaktadır ve çoğu zaten yeniden kabul edilmeyecektir. Öte yandan, müdahale yeterli sayıda yüksek riskli Konjestif Kalp Yetmezliği hastasını hedef almadığında hasta bakımını iyileştirmede olması gerektiği kadar etkili olmayacaktır.
Peki, hangi modelin optimal olduğunu nasıl belirleyeceğiz?
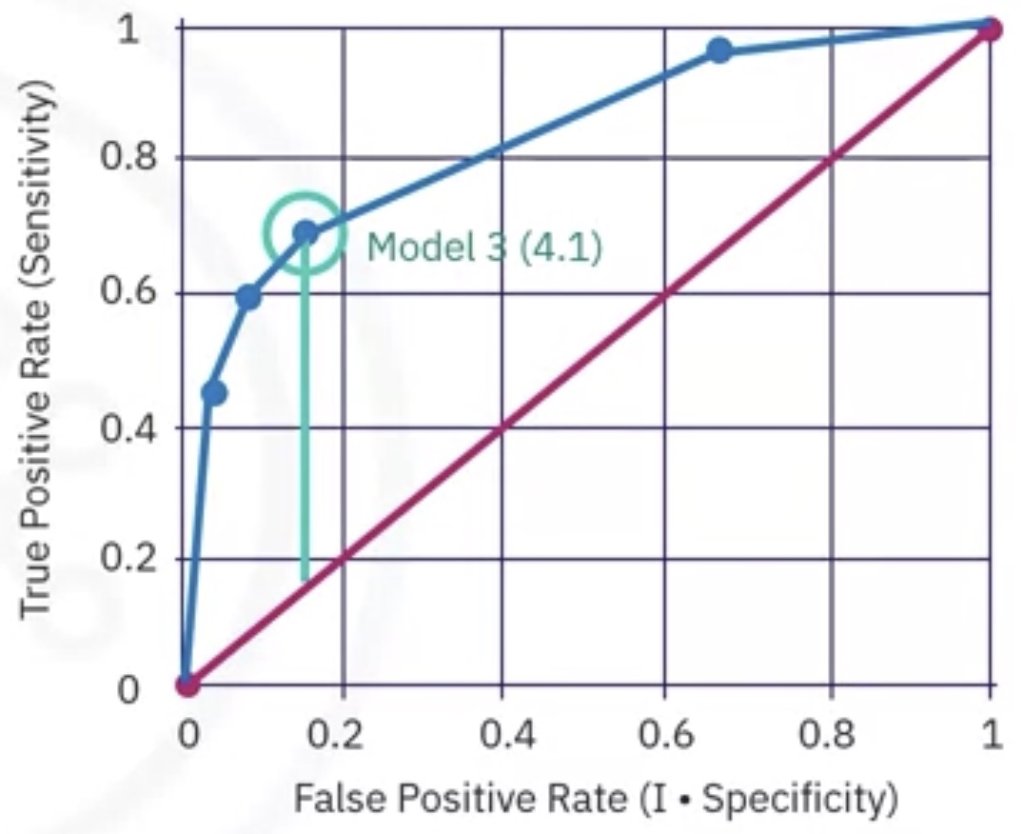
Bu slaytta görebileceğiniz gibi, en uygun model, kırmızı taban çizgisine göre mavi ROC eğrisi arasında maksimum ayrımı veren modeldir. Bu durumda; 3. modelin yani göreceli yanlış sınıflandırma maliyeti 4:1(4’e 1) olan modelin tüm modeller arasında en iyisi olduğunu görebiliriz.
ROC eğrisi, günümüzde makine öğrenimi ve veri madenciliğinde yaygın olarak kullanılmaktadır. ROC eğrisi, optimal sınıflandırma modelini belirlemede yararlı bir tanı aracı olacaktır. Bu eğri, bir ikili sınıflandırma modelinin ne kadar iyi performans gösterdiğini ölçer, bazı ayrım kriterleri değiştiğinde “evet” ve “hayır” çıktılarının sınıflandırmasını kaldırır. Bizim örneğimizde, kriter göreceli bir yanlış sınıflandırma maliyetidir. Göreceli yanlış sınıflandırma maliyetinin farklı değerleri için ROC eğrisi doğru-pozitif oranını yanlış-pozitif oranına karşı çizerek optimal modelin seçilmesine yardımcı oldu.
Uygulama:
Bu konuda da daha önceki konularda üzerinde çalıştığımız tarifler verisi ile uygulamamıza devam edelim ve Model Oluşturma ile Modeli değerlendirme aşamalarını uygulayalım.
Öncelikle model değerlendirme aşamasında kullanacağımız rastgele sayı oluşturma kütüphanesini ekliyoruz. Diğer kütüphaneleri önceki uygulamalarımızda eklemiştik zaten, eğer bağımsız bir şekilde direkt bu uygulamayı kodlayacaksanız onları da aşağıdaki şekilde ekleyelim.
import pandas as pd # Veriyi okumak için pandas kütüphanesini ekler
pd.set_option("display.max_columns", None)
import numpy as np # veri ile çalışmak için numpy kütüphanesini ekler
import re # metin verisi ile çalışmak için Regex kütüphanesini ekler
import random # bu çalışmaya özel ihtiyaç duyduğumuz rastgele sayı üreten kütüphaneyi eklerDaha önce modelleme için Karar Ağacı(Decision Tree) kullanacağımızdan bahsetmiştik. Bunun için scikit-learn kütüphanesini kodumuza ekleyeceğiz.
# Karar ağacı modellemesi için scikit-learn kütüphanesini ekleyelim %matplotlib inline from sklearn import tree from sklearn.metrics import accuracy_score, confusion_matrix import matplotlib.pyplot as plt !conda install python-graphviz --yes import graphviz from sklearn.tree import export_graphviz import itertools
Şimdi tekrar verimizi kontrol edelim;
tarifler.head()
Kodun çıktısı;
Burada, Asya (Kore, Japon, Çin, Tayland) ve Hint mutfaklarından sadece bazılarına ait tarifler için bir karar ağacı oluşturuyoruz. Bunu yapmamızın nedeni, verilerin bir mutfağa veya daha önce bahsettiğimiz gibi Amerikan mutfağından çok sayıda tarif içermesi nedeniyle bir grup mutfağa karşı ağırlıklı olması durumunda karar ağacının iyi çalışmamasıdır. Amerikan mutfaklarını analizimizin dışında tutabilir veya verilerin farklı alt kümeleri için karar ağaçları oluşturabiliriz. Biz çalışmamız için ikinci çözümü tercih edelim. Asya ve Hint mutfaklarına ilişkin verileri kullanarak karar ağacımızı oluşturalım ve karar ağacımıza dogu_agaci adını verelim.
# Ülke mutfaklarına ait alt mutfakları seçelim
asya_hint_mutfaklari = tarifler[tarifler.cuisine.isin(["korean", "japanese", "chinese", "thai", "indian"])]
mutfaklar = asya_hint_mutfaklari["cuisine"]
malzemeler = asya_hint_mutfaklari.iloc[:,1:]
dogu_agaci = tree.DecisionTreeClassifier(max_depth=3)
dogu_agaci.fit(malzemeler, mutfaklar)
print("Karar ağacı modeli dogu_agaci adıyla kaydedildi!")Şimdi de karar ağacının grafiğini çizelim ve nasıl göründüğüne göz atalım;
export_graphviz(dogu_agaci,
feature_names=list(malzemeler.columns.values),
out_file="dogu_agaci.dot",
class_names=np.unique(mutfaklar),
filled=True,
node_ids=True,
special_characters=True,
impurity=False,
label="all",
leaves_parallel=False)
with open("dogu_agaci.dot") as dogu_agaci_resmi:
dogu_agaci_grafigi = dogu_agaci_resmi.read()
graphviz.Source(dogu_agaci_grafigi)Kodun çıktısı;
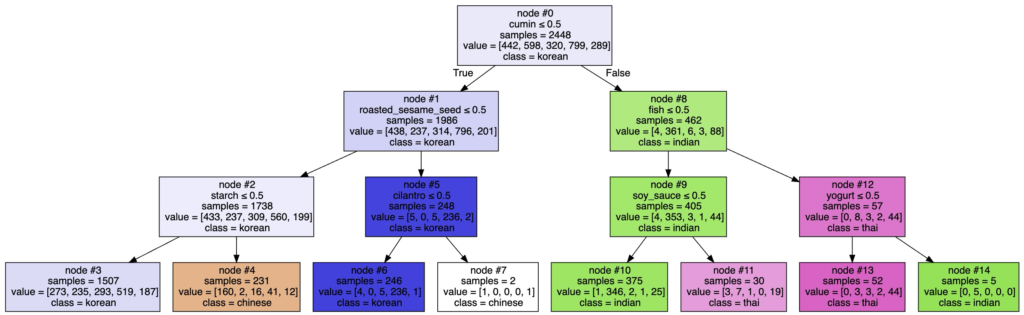
Bu karar ağacını şu şekilde yorumlayabiliriz;
Eğer tarif kimyon(cumin) ve balık(fish) içeriyorsa, yoğurt(yoghurt) içermiyorsa, muhtemelen bir Tayland Mutfağı tarifidir.
Eğer tarif kimyon(cumin) içeriyor ama balık(fish) ya da soya sosu(soy_sauce) içermiyorsa, muhtemelen bir Hint Mutfağı tarifidir.
Farklı tariflerin ait olduğkları mutfağı belirlemek için benzer kurallar bulmak üzere ağacın geri kalan dallarını analiz edebilirsiniz.
Ayrıca; benzer şekilde mutfakların başka bir alt kümesini seçerek ona ait tariflerden oluşan bir karar ağacı oluşturabilirsiniz. Örneğin, bazı Avrupa mutfaklarını seçebilir ve bu mutfakları farklılaştıran malzemeleri keşfetmek için karar ağaçları oluşturabilirsiniz.
Şimdi Model Değerlendirme aşamasında neler yapacağımıza bakalım. Yukarıda kullandığımız Asya-Hint Mutfağı modelimizi değerlendirmek için, veri setini eğitim seti ve test seti olarak bölmeliyiz. Sonra eğitim setini kullanarak karar ağacını kuracağız. Ardından, modeli test seti üzerinde test edecek ve modelin tahmin ettiği mutfakları gerçek mutfaklarla karşılaştıracağız.
İlk olarak sadece Asya ve Hint mutfakları ile ilgili verilerden oluşan yeni bir veri çerçevesi(dataframe) oluşturup buna dogu adını verelim.
dogu = tarifler[tarifler.cuisine.isin(["korean", "japanese", "chinese", "thai", "indian"])]
Şimdi bu seçtiğimiz mutfaklarda kaç tarif olduğuna göz atalım;
dogu["cuisine"].value_counts()
Kodun çıktısı;
cuisine
korean 799
indian 598
chinese 442
japanese 320
thai 289
Her mutfağa ait tarifler içinden rastgele 30 tarifi test seti olarakçıkartalım ve dogu_test olarak adlandıralım;
# Veri boyutunu belirleyelim
sample_n = 30
# Her mutfaktan 30 tarif alalım
random.seed(1234) # rastgele sayı üretelim
dogu_test = dogu.groupby("cuisine", group_keys=False).apply(lambda x: x.sample(sample_n))
dogu_test_malzemeler = dogu_test.iloc[:,1:] # malzemeler
dogu_test_mutfaklar = dogu_test["cuisine"] # karşılık gelen mutfaklarŞimdi kodumuzu bir kontrol edelim ve her mutfakta 30 tarif olduğunu görelim;
# her mutfakta 30 tarif olduğunu görelim dogu_test["cuisine"].value_counts()
Kodun çıktısı;
cuisine
chinese 30
indian 30
japanese 30
korean 30
thai 30
Şimdi de eğitim setimizi oluşturalım. bunun için dogu veri setimiz içinden test verisi olarak ayırdığımız 30 tarifi çıkartıyoruz ve dogu_egitim olarak isimlendiriyoruz.
dogu_test_index = dogu.index.isin(dogu_test.index) dogu_egitim = dogu[~dogu_test_index] dogu_egitim_malzemeler = dogu_egitim.iloc[:,1:] # malzemeler dogu_egitim_mutfaklar = dogu_egitim["cuisine"] # karşılık gelen mutfaklar
Şimdi yapacağımız kontrolde eğitim veri setimizin tarif sayılarının önceki dogu veri setimizden 30 eksik olduğunu görmeliyiz;
dogu_egitim["cuisine"].value_counts()
Kodun çıktısı;
cuisine
korean 769
indian 568
chinese 412
japanese 290
thai 259
Bu adımda, eğitim setimizi kullanarak karar ağacı oluşturacağız. Bu yeni karar ağacını da dogu_egitim_agaci olarak isimlendirelim;
dogu_egitim_agaci = tree.DecisionTreeClassifier(max_depth=15)
dogu_egitim_agaci.fit(dogu_egitim_malzemeler, dogu_egitim_mutfaklar)
print("dogu_egitim_agaci isimli karar ağacı modeliniz oluşturulmuştur!")Şimdi bu karar ağacına göz atalım;
export_graphviz(dogu_egitim_agaci,
feature_names=list(dogu_egitim_malzemeler.columns.values),
out_file="dogu_egitim_agaci.dot",
class_names=np.unique(dogu_egitim_mutfaklar),
filled=True,
node_ids=True,
special_characters=True,
impurity=False,
label="all",
leaves_parallel=False)
with open("dogu_egitim_agaci.dot") as dogu_egitim_agaci_resmi:
dogu_egitim_agaci_grafigi = dogu_egitim_agaci_resmi.read()
graphviz.Source(dogu_egitim_agaci_grafigi)Kodun çıktısı;
Grafiğin okunabilir olması için üzerine tıkladığınızda yeni sekmede açılacaktır. Ancak gördüğünüz gibi oldukça büyük bir grafik olduğu için mouse’unuz ile sağa ve aşağıya doğru kaydırarak keşfedebilirsiniz.
Şimdi modelimizi test verisi ile test edelim;
dogu_mutfaklar_tahmini = dogu_egitim_agaci.predict(dogu_test_malzemeleri)
Karar ağacının her bir tarifin mutfağını ne kadar doğru belirleyebildiğini ölçmek için, her bir mutfaktan kaç tarifin doğru sınıflandırıldığına dair güzel bir özet sunan bir Karışıklık Matrisi(Confusion Matrix) oluşturacağız. Bu matris ayrıca hangi mutfakların başka hangi mutfaklarla karıştırıldığına da ışık tutuyor.
test_mutfaklari = np.unique(dogu_test_mutfaklar)
dogu_karisiklik_matrisi = confusion_matrix(dogu_test_mutfaklar, dogu_mutfaklar_tahmini, labels = test_mutfaklari)
title = 'Doğu Mutfakları Karışıklık Matrisi(Confusion Matrix)'
cmap = plt.cm.Blues
plt.figure(figsize=(8, 6))
dogu_karisiklik_matrisi = (
dogu_karisiklik_matrisi.astype('float') / dogu_karisiklik_matrisi.sum(axis=1)[:, np.newaxis]
) * 100
plt.imshow(dogu_karisiklik_matrisi, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(test_mutfaklari))
plt.xticks(tick_marks, test_mutfaklari)
plt.yticks(tick_marks, test_mutfaklari)
fmt = '.2f'
thresh = dogu_karisiklik_matrisi.max() / 2.
for i, j in itertools.product(range(dogu_karisiklik_matrisi.shape[0]), range(dogu_karisiklik_matrisi.shape[1])):
plt.text(j, i, format(dogu_karisiklik_matrisi[i, j], fmt),
horizontalalignment="center",
color="white" if dogu_karisiklik_matrisi[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('Doğru Etiketler')
plt.xlabel('Tahmini Etiketler')
plt.show()Kodun çıktısı;
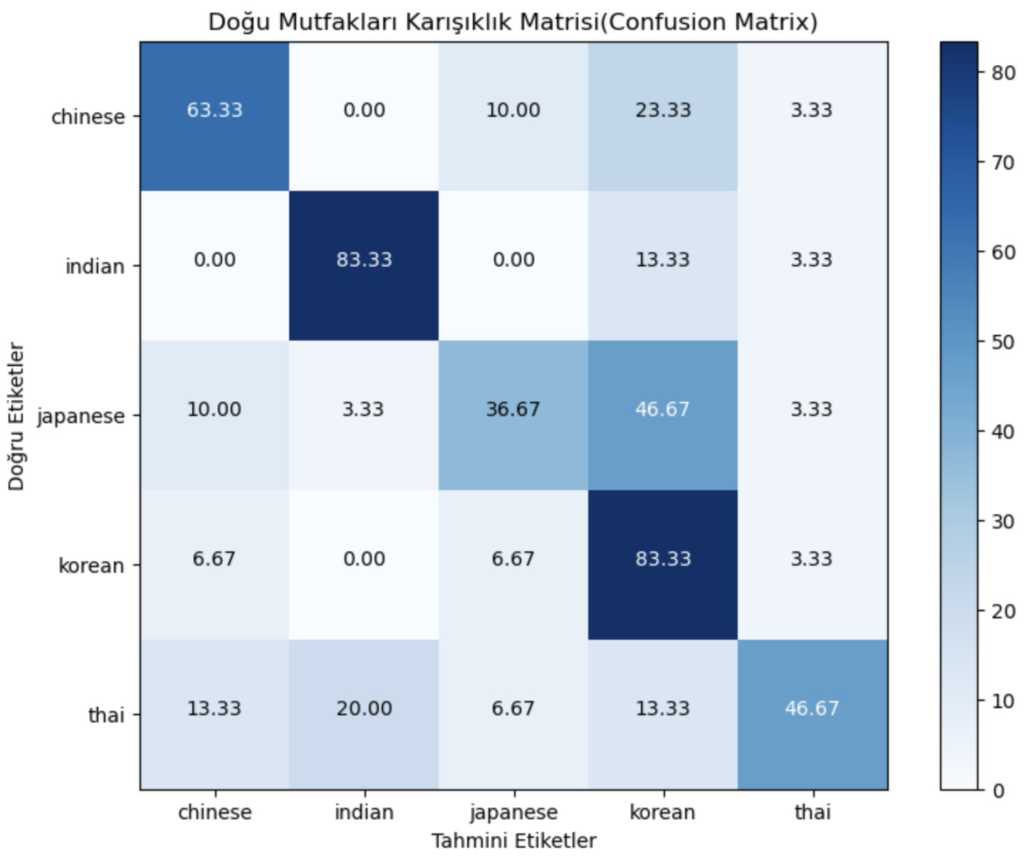
Satırlar veri kümesindeki gerçek mutfakları, sütunlar ise tahmin edilen mutfakları temsil eder. Her satırın toplamı %100 olmalıdır. Bu karışıklık matrisine göre aşağıdaki gözlemleri yapabiliriz:
- Karışıklık matrisindeki ilk satıra göz attığımızda görüyoruz ki, dogu_test verisi içindeki Çince tariflerin %60’ı karar ağacımız tarafından doğru sınıflandırılırken, Çince tariflerin %37’si Kore ve %3’ü Hint Mutfağı olarak yanlış sınıflandırılmıştır.
- Hint satırına göz attığımızda ise, dogu_test verisi içindeki Hint tariflerinin %77’si karar ağacımız tarafından doğru sınıflandırılmış, ancak Hint tariflerinin %3’ü Çin, %13’ü Kore ve %7’si Tayland olarak yanlış sınıflandırılmıştır.
Karar ağacımızı, eğitim setindeki verilerin rastgele örneklenmesini kullanılarak oluşturduğumuz için, aynı eğitim setini kullanarak bile karar ağacını her yeniden oluşturduğunuzda aynı sonuçların alınamayabileceğini lütfen unutmayın. Yani, yukarıdaki kodları kendiniz denerken karışıklık matrisinizde yukarıda gösterilenlerden farklı sayılar elde ederseniz endişelenmeyin.
Terim Sözlüğü:
| Terim | Açıklama |
|---|---|
| İkili Sınıflandırma Modeli(Binary classification model) | Verileri evet/hayır gibi iki kategoriye ayıran bir model. |
| Veri Derleme(Data compilation) | Modelleme için gerekli verilerin toplanması ve düzenlenmesi süreci. |
| Veri Modelleme(Data modeling) | Veri bilimi metodolojisinde, veri bilimcilerin belirli soruları yanıtlamak için tanımlayıcı veya tahmine dayalı modeller geliştirdiği aşama. |
| Tanımlayıcı Model(Descriptive model) | Değişkenler arasındaki ilişkileri inceleyen ve gözlemlenen örüntülere dayalı çıkarımlar yapan bir model türü. |
| Tanısal Ölçümlere Dayalı Ayarlama(Diagnostic measure based tuning) | Tanısal ölçümlere ve performans göstergelerine dayalı olarak parametreleri ayarlayarak modele ince ayar yapma süreci. |
| Tanısal Ölçümler(Diagnostic measures) | Modelin amaçlandığı gibi çalıştığından emin olmak için bir modelin performansının değerlendirilmesi. |
| Ayrıştırma Kriteri(Discrimination criterion) | Modelin farklı sonuçları sınıflandırmadaki performansını değerlendirmek için kullanılan bir ölçü. |
| Hatalı Pozitif Oranı(False-positive rate) | Modelin negatif sonuçları yanlışlıkla pozitif olarak tanımlama oranı. |
| Histogram | Verilerin aralıklara veya kutulara bölündüğü ve her bir çubuğun yüksekliğinin o aralığa düşen veri noktalarının sıklığını veya sayısını temsil ettiği bir veri kümesinin dağılımının grafiksel gösterimi. |
| Maksimum Ayrılma(Maximum separation) | ROC eğrisinin doğru-pozitif ve yanlış-pozitif oranları arasında en iyi ayrımı sağladığı nokta, en etkili modeli gösterir. |
| Model Değerlendirme(Model evaluation) | Dağıtımdan önce modelin kalitesini ve uygunluğunu değerlendirme süreci. |
| En İyi Model(Optimal model) | ROC eğrisi ile taban çizgisi arasında maksimum ayrımı sağlayan model, daha yüksek doğruluk ve etkinliği gösterir. |
| Alıcı İşletim Karakteristiği(Receiver Operating Characteristic) (ROC) | Başlangıçta askeri radar için geliştirilen bu istatistiksel eğri, ikili sınıflandırma modellerinin performansını değerlendirmek için kullanılmıştır. |
| Göreceli Yalış Sınıflandırma Maliyeti(Relative misclassification cost) | Bu ölçüm, model oluşturmada doğru-pozitif ve yanlış-pozitif oranları arasındaki dengeyi ayarlamak için kullanılan bir parametredir. |
| ROC Eğrisi (ROC curve) | Optimum sınıflandırma modelinin performansını belirlemek için kullanılan bir teşhis aracı. |
| Ayırma(Separation) | Ayırma, modelin sonuçları doğru bir şekilde sınıflandırmada elde ettiği ayrıştırma derecesidir. |
| İstatistiksel Anlamlılık Testi (Statistical significance testing) | Verilerin model içinde uygun şekilde ele alındığını ve yorumlandığını doğrulamak için değerlendirme tekniği. |
| Doğru Pozitif Oranı (True-positive rate) | Modelin olumlu sonuçları doğru bir şekilde tanımlama oranı. |


Bağlantıda Kalalım